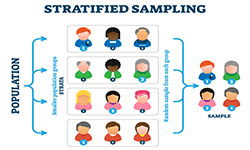
If you want to conduct a study and are not willing or able to question an entire population, sampling is a very efficient methodology to still gain valid results. The sample, however, needs to represent the whole population, which is why you need to carefully avoid sampling bias. To gain that kind of representativeness, stratified sampling is a good way to achieve a distinguished sample to work with. The following article will show you how stratified sampling works and how you use it correctly.
Definition: Stratified sampling
Stratified sampling involves dividing the population into homogeneous subgroups or ‘strata‘, based on certain characteristics, and then randomly drawing samples from each stratum. It aims to enhance the precision of a sample and ensures that various characteristics within a population are equally studied, reducing sampling bias and improving the accuracy of results. Strata can be divided by age, gender, status, income and many other factors or even combination of these, depending on the aims of the study.
How to use stratified sampling
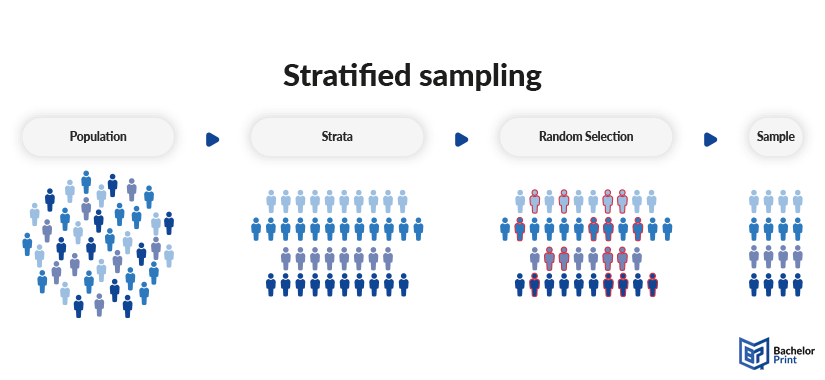
Stratified sampling involves a whole process of defining strata and sampling participants, where each step is essential to the study.
1. Defining the population
The first step of any sampling method is clearly defining the population you’ll study. Stratified sampling is no different, and it takes the following forms:
- Choosing characteristics for subgrouping
Once you’ve defined your population, explain what the subgroups would look like. Choose the characteristics that will differentiate your subgroups and divide the population into the relevant groups.
When choosing the characteristics, it’s essential to note that each population member belongs to a single subgroup. Also, the classification of each item to each subset should be clear and conspicuous.
- Multiple characteristics
You can also divide your population using multiple characteristics if you group every member into one subgroup. However, to get the overall number of subgroups, you should multiply the number of subgroups for each factor.
2. Separating the population
Next, assort all members and group them into a stratum. Ensure that each stratum has no overlap, is mutually exclusive, and represents the entire population when put together.
When you combine these characteristics, you get nine groups in total. You must assign each employee to one subgroup, as shown in the table below:
3. Deciding the sample size
Thirdly, decide your total sample size, which must adequately draw practical statistical conclusions from each subgroup. Use the sample size calculator to estimate numbers when you have errors, such as the desired margin error, standard deviation, confidence level, and estimated size.
4. Random sampling
Lastly, you can use simple random sampling for items within each stratum. Using random sampling in a stratified sampling method allows you to get samples representing that particular subgroup.
Advantages
Stratified sampling is a statistical tool in research, as it ensures representation of the entire population in a very strategic and thus easier way. The following advantages of stratification will further illustrate why stratified sampling is so important.
- Very accurate representation due to the strata. When the population is divided into groups, you make sure that every part of the population is represented by one stratum and when you sample from those strata randomly, there is less room for any sampling bias.
- More precision. As each member of a population can be sorted into only one stratum, you eliminate overlap between different participants and avoid missing out on other groups.
- Reduced efforts in analysis. Having more precise strata also means that there is no need for a large sample. With fewer participants in the study, it is more cost and time efficient.
Disadvantages
Even the best research methods are not flawless, which is why stratified sampling also has its disadvantages, which will be listed below.
- Limited applicability. If the studied population cannot be definitely divided into subgroups because there is no exact list of each member of a population, the strata are not sure to represent the entire population and thus the study loses validity.
- Possible overlap. If the strata are not defined so that each member of the population fits into only one of them, the overlap makes the samples are likely to misrepresent the whole.
- Strata can be biased. There is also a possibility that the researcher subconsciously introduces bias while defining the strata. It can happen that the characteristics determining the strata influence the results of the study and thus introduce bias.
- Preparation can take a lot of time. As the strata need to be defined first, this process can take a lot of time to produce a representative sample.
Proportionate vs. disproportionate sampling
In the process of stratified sampling, the researcher furthermore needs to decide on whether they want to sample proportionately or disproportionately. In proportionate sampling, the samples from each stratum are sized according to the population demographics. The sample size from each stratum is calculated with the following formula.
(Sample size/population size) x stratum size = stratum sample
The sample size here refers to the number of people you want to participate in your study, whereas the stratum size is the number of people in the according stratum. An example calculation could look like this:
In disproportionate sampling, there is no such formula. The researcher themselves decides how many samples they take of each group. This can mean they sample the same number of participants from each stratum, or they take a quarter of the men and half of the women. Disproportionate sampling is thus more likely to be biased.
Simple random sampling vs. Stratified sampling
Simple random sampling is a type of sampling where the participants are chosen randomly from the entire population. In the case of a stratified sample, the population is divided into subgroups first before participants are sampled from the strata. However, the process of stratified sampling might as well include simple random sampling at the end. After the strata are determined, the study participants are often sampled randomly from each stratum.
Simple random sampling is also mostly applied when stratified sampling is not possible due to the size and extent of the population or a lack of information about it. Generally, stratified sampling is more reliable and representative but also more time and cost intensive.
FAQs
In stratified sampling, the population is first divided into separate subgroups, the strata, before participants are sampled randomly from each stratum.
Stratified sampling involves a lot of time and effort, especially in the process of establishing strata. Furthermore, the characteristics which determine the strata can end up biasing the study if they are not chosen carefully. Lastly, if the entire population cannot be listed or precisely determined, the strata will not be valid because there is no guarantee that they represent the population as a whole.
In simple random sampling, you select the participants directly from the population without verifying their characteristics. In stratified sampling, you divide the population into subgroups of the same characteristics and sample participants from those, ensuring equal representation of each group in the study.
