
As a core component of statistics, the t-test offers a robust means of comparing group averages and discerning the importance of their differences. This inferential statistic, used to determine significant variations, employs a test statistic for hypothesis testing. It proves particularly useful when dealing with data sets of unknown variances and normal distributions, like outcomes from a hundred coin tosses.
Definition: T-test
T-statistics compare the means of two samples using statistical analysis. It is used in hypothesis testing with the null hypothesis (where the difference between the group means is zero) and the alternate hypothesis (the difference is not equal to zero).
When data sets have a normal distribution, but you are unsure about the variance of the population, the t-statistical test is typically utilized. For instance, you might flip a coin 1,000 times and discover that the frequency of heads is distributed generally throughout all trials.
When to use a t-test
An appropriate sample size, homogeneity of variance, ratio data or interval data measurements, simple random extraction, and normal distribution of data are all prerequisites for performing a t-test.
What type of t-test should be used?
There are different types of t-tests: one-sample, two-sample, or paired t-test. These will be introduced and explained in the next paragraphs.
One-sample, two-sample, or paired t-test
| One-sample t-test |
| • The test assesses whether there is a significant difference between the sample mean and the population mean. |
| • In situations where the population standard deviation is unknown, one-sample t-testing is applied. |
| • When the sample size is significantly small, the test is also applied. |
| Two-sample t-test |
| • Also called an independent sample test, it is often performed to verify the equality of two population means. |
| • One frequent use is to determine whether a novel method or therapy is better than an existing one. |
| • There are several variations in this test. The data may either be paired or not paired. |
| • One of the most limiting underlinings of this test is that it may be compromised if the data contradicts the assumptions. |
| Paired t-test |
| • To compare the means of two related samples. |
One-tailed or two-tailed t-test
One-tailed t-test
- Also called the directional test, this is a statistical technique used to determine if a sample of data significantly deviates from the theoretical mean.
- When a directed hypothesis – one that predicts that the model mean will be either greater or less than the theoretical mean – is present, a one-tailed test is employed to evaluate the hypothesis.
A two-tailed t-test
- It is a statistical test performed when there is a significant difference between the means of two groups.
- When there is no difference between the means of the two groups, the null hypothesis is tested using this method.
- The other possibility is that the two groups significantly diverge from one another.
Performing a t-test
The t-score for an independent t-testing is:
- T equals the mean of population 1 minus the mean of population 2 divided by the product of the pooled standard deviation and the square root of one over the sample size of sample 1 plus one over the sample size of sample 2.
To calculate, the following steps ought to be keenly adhered to:
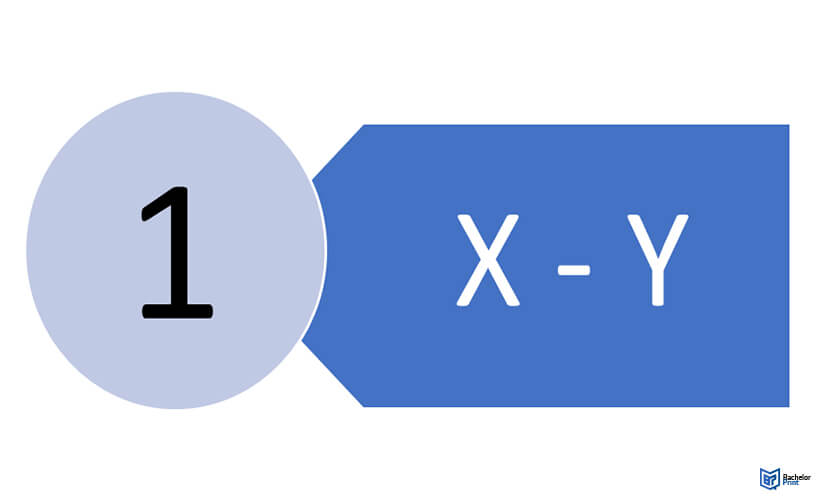
Step 1
Subtract each Y value from each X value.

Step 2
Sum up the values from Step 1 and set this number aside for the final calculation.
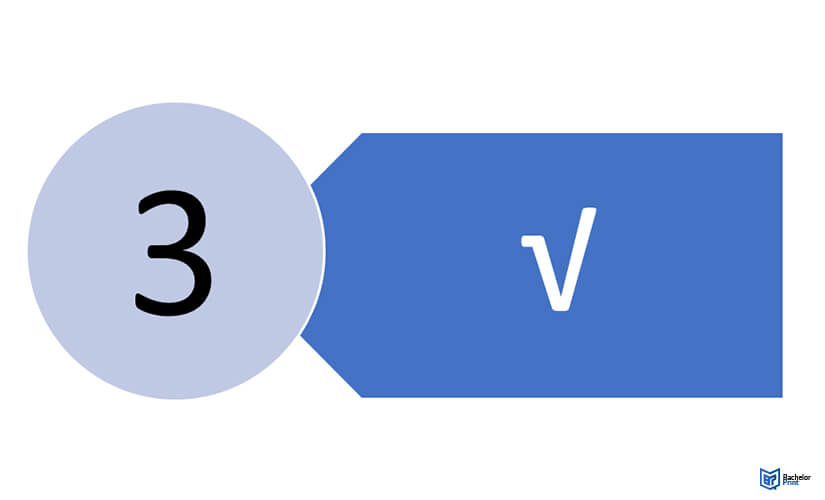
Step 3
Square the solution from Step 1.
Step 4
Sum the squared differences from Step 3.

Step 5
Use the formula explained above to calculate the t-score.
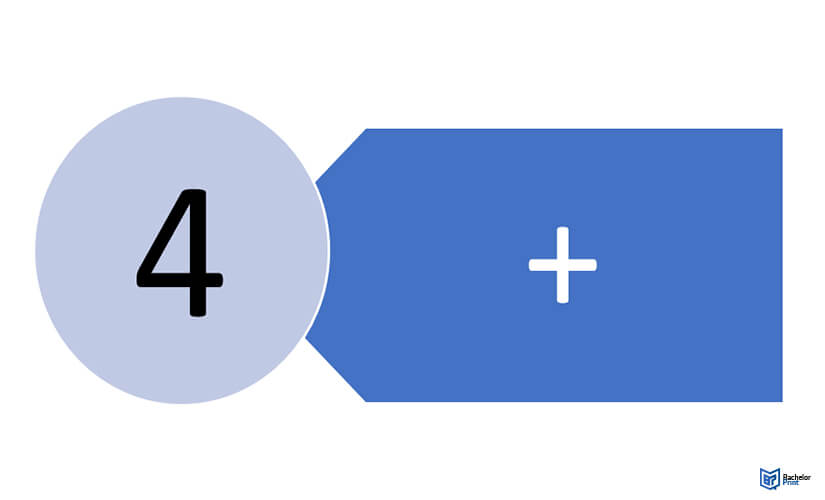
Step 6
Subtract one from the sample size to get the degrees of freedom.

Step 7
Locate the p-value in the t-table, using the degrees of freedom, in Step 6.

Step 8
Compare the t-table value from Step 7 to the calculated t-value.
Interpreting t-test results
The statistical significance and practical significance of the t- statistical test results can be used to interpret the findings. A t-results test might be interpreted according to its level of significance, where the p-value indicates the likelihood that the mean difference is the result of chance.3 Also, the significance of the difference increases with decreasing p-value.
A t-statistical test’s results can also be evaluated in terms of their relevance in real-world situations. The practical significance of the difference is determined by the effect size, calculated by dividing the mean difference by the standard deviation. The difference has greater practical significance the larger the effect magnitude.
Presenting the results of a t-test
A table or graph can be used to display the outcomes of a t-test. The means of the two groups being compared, the standard deviations of the two groups, the test statistic, the degrees of freedom, and the p-value should all be included when presenting the findings of a t-test in a table.
What’s more, when presenting the t-testing results, the mean of each group should be represented by a line, the standard deviation by a shaded region surrounding the line, and the p-value should be displayed on the graph.
numerous advantages for Canadian students:
- ✓ 3D live preview of your configuration
- ✓ Free express delivery for every order
- ✓ High-quality bindings with individual embossing

FAQs
When conducting a t-test, it is typical to make assumptions about the random sampling, appropriate sample size, measurement scale, normality of the data distribution, and equality of variance in standard deviation.
T-testing is used by businesses to assess whether two different means belong to the same population.
Additionally, it enables organizations to comprehend how likely it is that their outcomes are only accidental.
Test drawbacks include sensitivity to sample size, being less resistant to breaches of the equal variance and normality assumptions when sample sizes are inequitable, and performing better with higher sample numbers.
Additionally, there are a number of assumptions made by t-testing that could not hold true in actual usage.
Sources
1 Gerald, Banda. “A brief review of independent, dependent and one sample t-test.” International Journal of Applied Mathematics and Theoretical Physics 4, no. 2 (2018): 50-54.
2 Goulden, C. H. Methods of Statistical Analysis, 2nd ed. New York: Wiley, pp. 50-55, 1956.
3 Mishra, Prabhaker, Uttam Singh, Chandra M. Pandey, Priyadarshni Mishra, and Gaurav Pandey. “Application of student’s t-test, analysis of variance, and covariance.” Annals of cardiac anaesthesia 22, no. 4 (2019): 407.
