
In statistics, there are many ways to represent data and make it easier to understand. Diagrams serve this purpose by visualizing numbers, survey results, research findings, or complex concepts in general. One elementary diagram is the Venn diagram, which presents data inside of two or more overlapping circles. The following article provides an in-depth explanation of this type of diagram and its proper usage.
Definition: Venn diagram
A Venn diagram shows the relation between two or more sets through overlapping circles or ovals (in rare cases). They are mostly used in algebra to determine the overlap of two sets of numbers and are typically labelled with alphabetical letters starting from A. Venn diagrams have a wide range of applications, also showing the junction of non-numerical data sets.
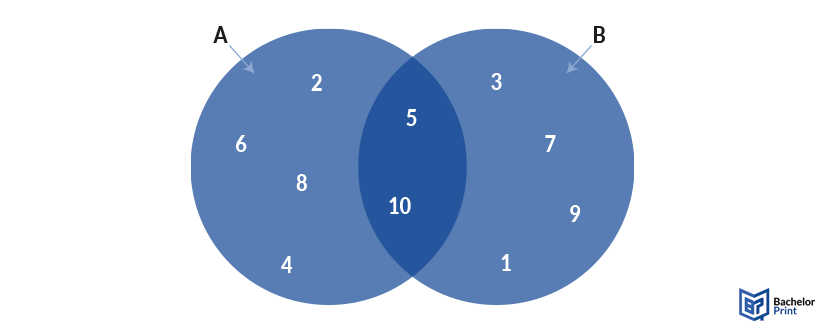
In this example, you can see the numbers from one to ten, divided into even and odd numbers, while the overlapping area includes all of them that are divisible by 5.
History
The theory behind the Venn diagram was founded by John Venn, an English logician, who strived to illustrate the frequency theory of probability in 1866. In combination with algebra, he developed the concept of sets as visual units, which then led to the birth of the Venn diagram. However, the name itself was not mentioned until 1918, when Clarence Lewis, an American philosopher, referred to the diagram as a Venn diagram in one of his books, “A Survey of Symbolic Logic.”
numerous advantages for Canadian students:
- ✓ 3D live preview of your configuration
- ✓ Free express delivery for every order
- ✓ High-quality bindings with individual embossing

Types of sets
Each circle that includes data is called a set, a defined part that fits into one category. However, there are a few terms to further differentiate these sets according to their characteristics.
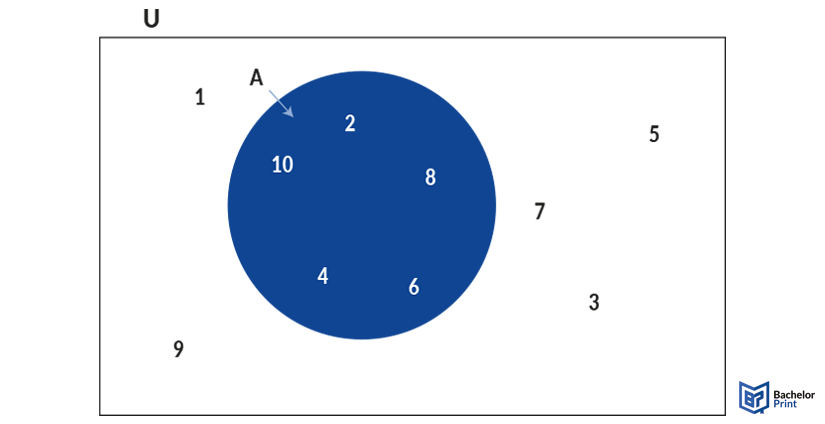
A universal set is the framework of the data. It is often visualized as a square, which contains all relevant sets. The universal set is usually defined by the letters E or U. U is more common here because E could also mean a normal set. In the following example, the universal set includes all numbers from one to ten, while the set contains only the even numbers.
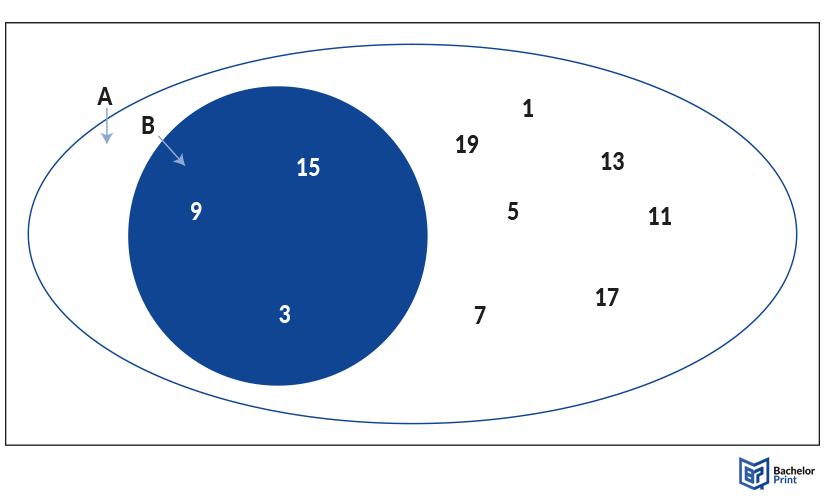
Subsets are sets that exist inside another set. This can happen when you build subcategories of your data to break it down further into simple units. The subset is then called an element of the higher-ranking set. In this example, set A includes all odd numbers up to twenty, while set B includes only those that are divisible by three.
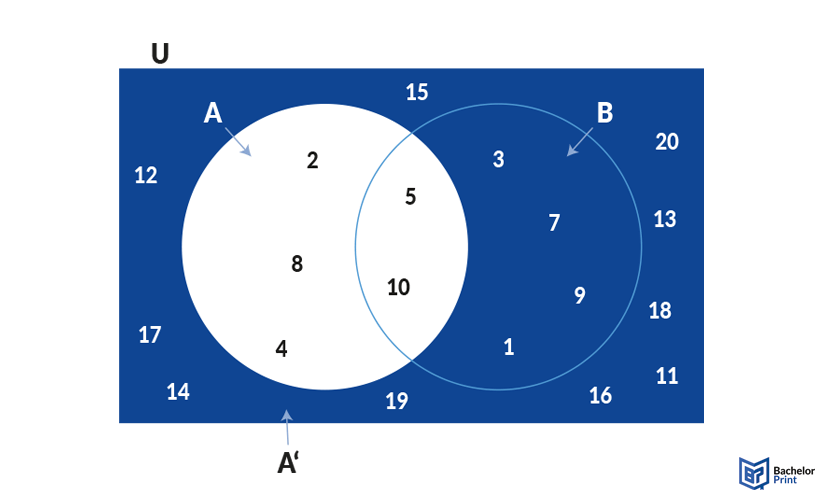
Complementary sets are sets that exclude each other. They are described with the letter of the set plus an apostrophe, for example, A’. Set A’ thus includes everything from U that is not A. In the following example, U includes all numbers from one to twenty, set A consists of only even numbers to ten, while set B consists of only odd numbers to ten. A’ subsequently is only even numbers between one and ten.
Disjoint sets are when two sets do not have any commonalities, meaning they do not overlap. It is pretty rare to see this in a Venn diagram because its purpose is to show the overlaps of different sets. So if they do not overlap, there is no need for the diagram in the first place. In theoretical exercises, it may sometimes be used to confuse students, or in reality, when you have to make a point about sets not overlapping.
Creating a Venn diagram
Creating a Venn diagram is not very difficult. The following steps will show you how to plan and draw the diagram and what important things you need to keep in mind.
1. Sort all items into categories, creating sets. Try to form as few sets as possible without losing clarity.
2. Define the rectangle (the universal set) and label it with the topic of your examination.
3. Now you can add the circles of your categories and fill them with the corresponding items. Here, you need to keep in mind that if you have more than 3 sets, you may need to restructure your diagram.
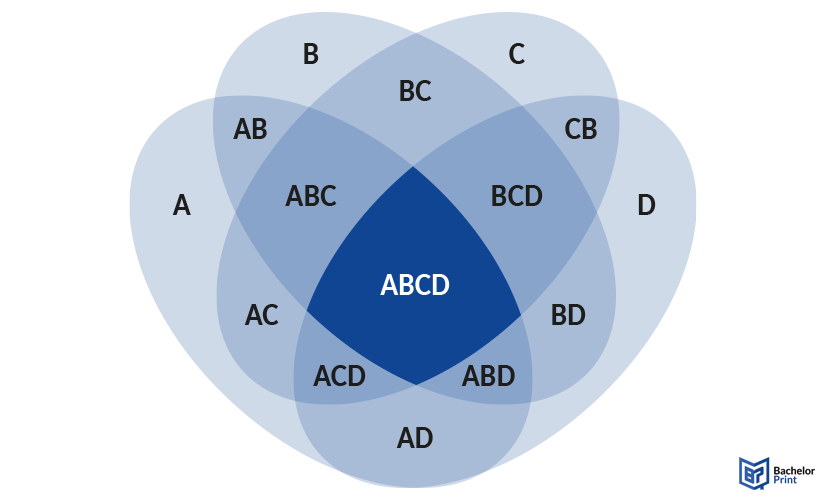
➜ To make sure every category overlaps with every other category, starting from 4 sets, you need to change the shape into ovals, as the following examples show.
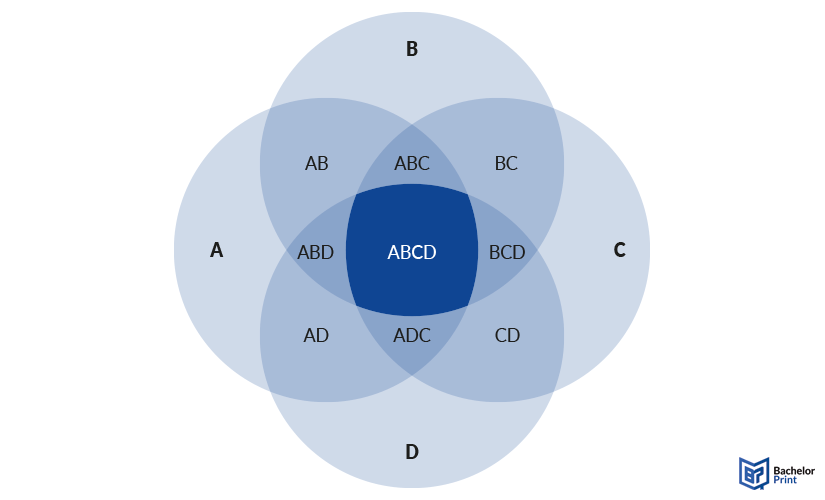
Looking at this image, you may realize that there is no area where only A and C overlap. Each set can only have single overlaps with its neighbors. These types of Venn diagrams can still be used, for example, for the Western adaptation of the Japanese concept of ikigai, which is one of the most famous ones.
For logical or more complex mathematical problems, however, you may use ellipses to create the diagram. Here you can see that every set has an overlap with each of the others.
Symbols
In mathematical Venn diagrams, five different symbols describe the relationship between sets.
Units
A∪B: The first one is “∪,” the union symbol. It signals that the unit of both sets is described. This is why we pronounce it “A union B.”
Intersection
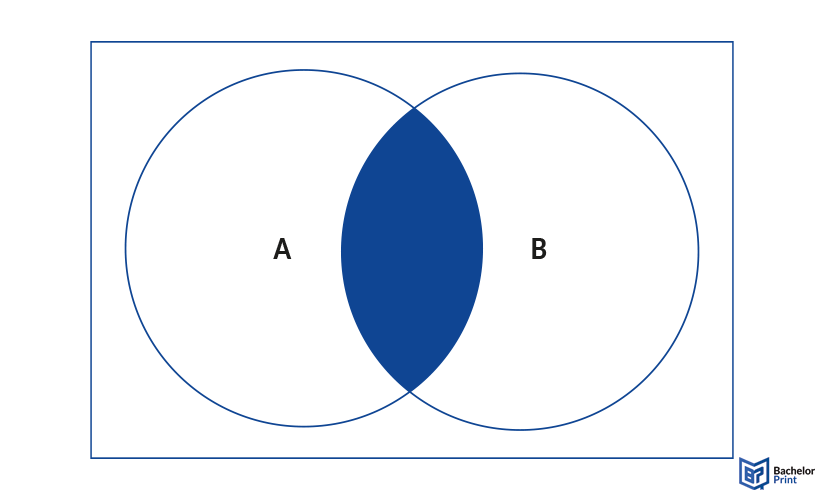
A∩B: The second symbol “∩” describes the junction and is thus read “A junction B.” The junction refers to only the overlap of both sets.
Inclusion
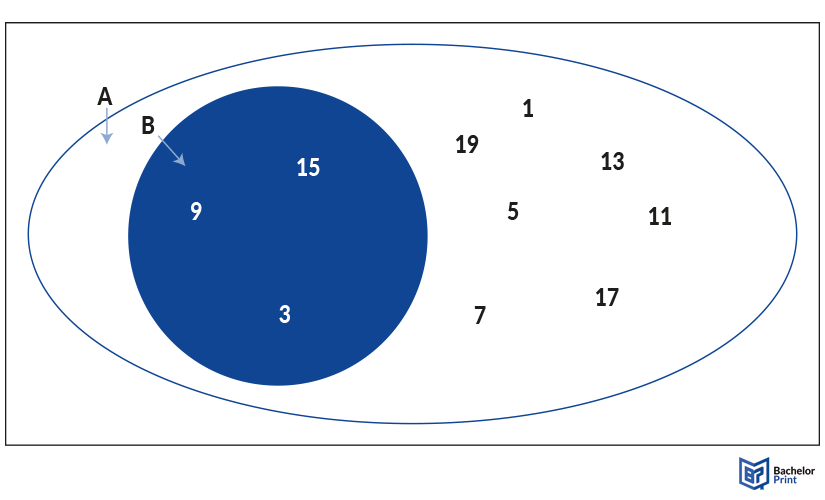
B⊂A: The third symbol “⊂” describes the inclusion of one set in another one, voiced out as “B is a subset of A.”
Exclusion
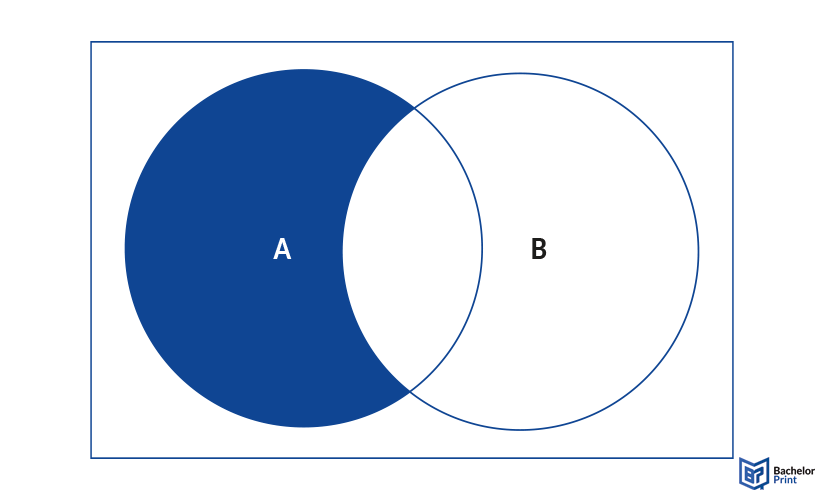
A\B: The fourth one is for when you want only data from one set without anything that overlaps with the other, thus called “A without B,” symbolized through “\.” Keep in mind that the sign is not the usual slash “/” but the one in the other direction.
Uniquity
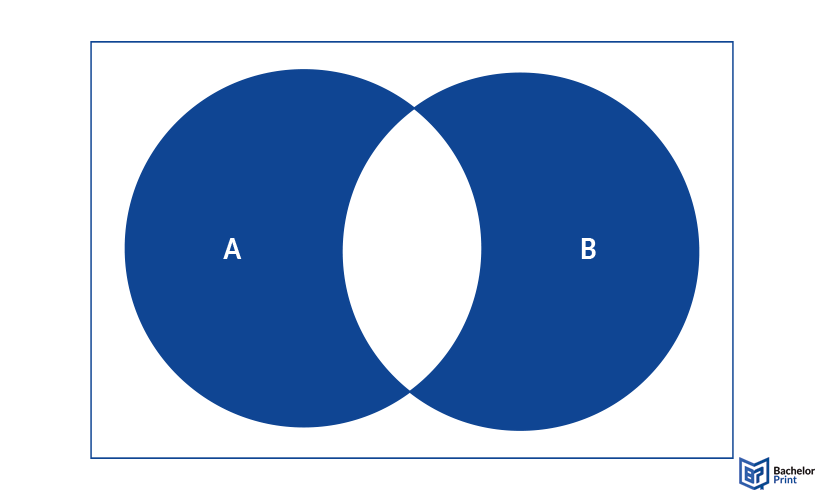
AΔB: When you want only data from sets A and B, which is solely unique to them and not in the overlapping section, this is described by “Δ” or “AuB \ AnB.”
Complementary sets
Furthermore, there are also complementary sets of each of these. The complementary set of A is A’, but it can also be written as Ā, which is why complementary sets are often described by their name with a line on top. The following examples will visualize this.
- The blue area is everything that is not A and thus Ā.
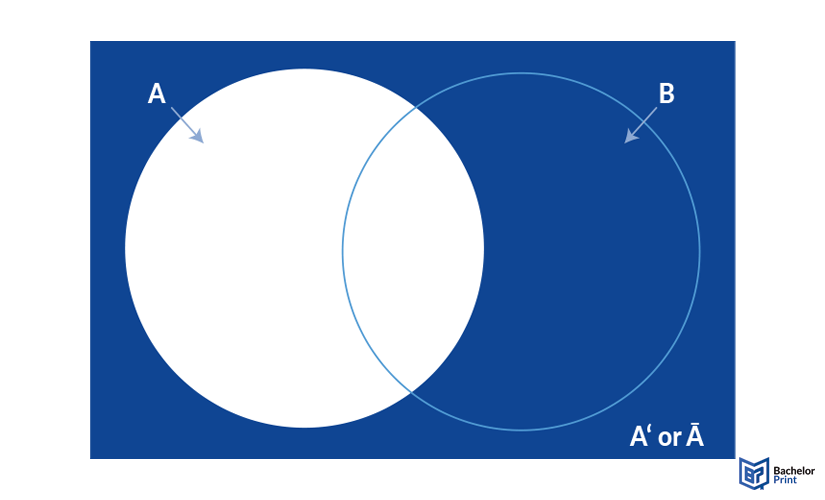
- Here, the blue area is everything but A∪B, and thus (A∪B)’ or also A’∩B’. This is because if you want the complementary set, you can either put the set in brackets and place the apostrophe behind it, or you can take the opposite of each set and turn the symbol around.
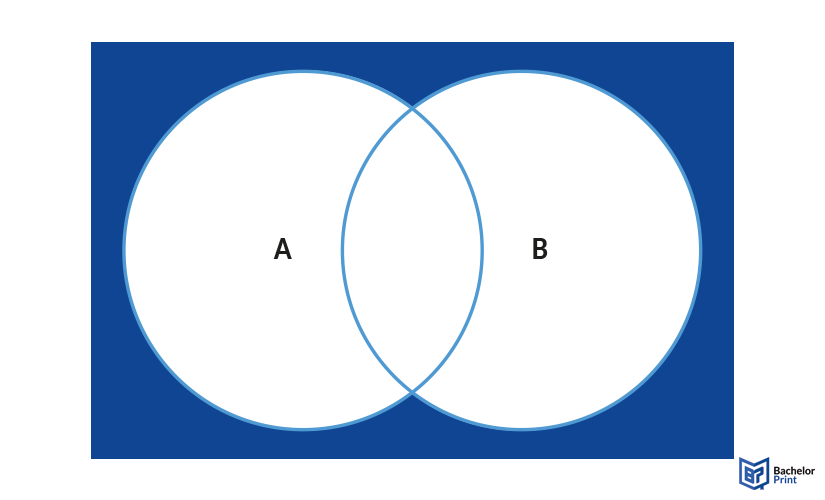
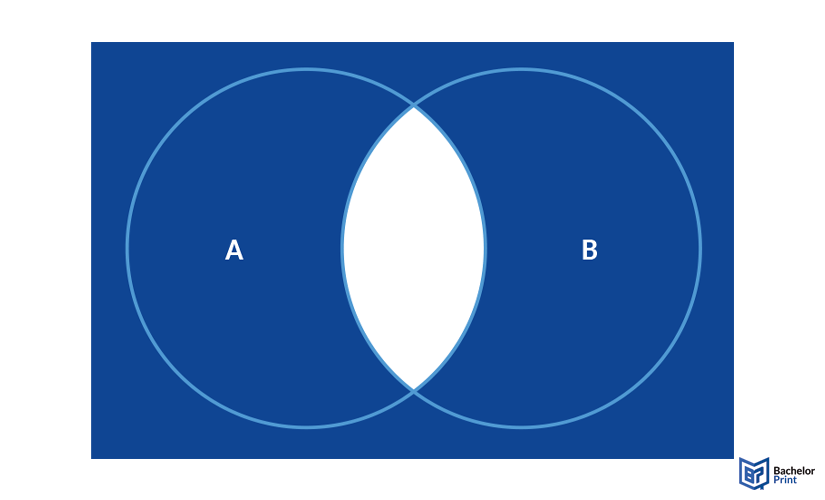
- The opposite of the junction works the same. You want everything but A∩B, so it is either (A∩B)’ or A’∪B’.
Use and purpose
Venn diagrams serve many purposes due to their great variety of possible applications.
- Venn diagrams can break down complex mathematical problems into smaller units, which can make them clearer and easier to solve.
- They draw logical connections between data sets, especially through the operators of units, intersections, elements, exclusion, and complementarity.
- They compare two or more options, making it easier to spot unique features and shared traits. In research, this simplifies selecting the right method.
- They display and organize information visually in a simple way. It is easy to find similarities and differences between sets or map them out in the first place. This holds for both simple and complex concepts.
Non-mathematical Venn diagrams
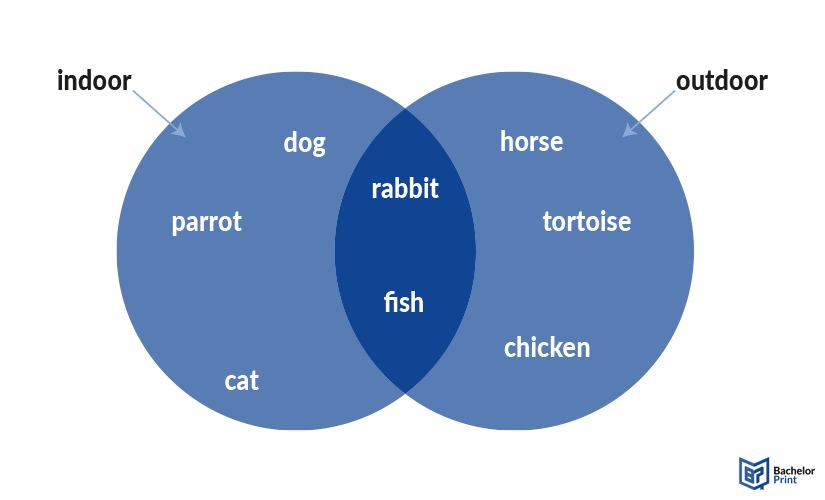
Not all Venn diagrams include numbers that show complex concepts in a simple way. The basis for every Venn diagram is to break down your data into categories and then examine their common ground. The following example shows this based on different pets.
Venn diagram vs. Euler diagram
Please note that this article refers to this type of diagram in general. There is a differentiation to the Euler diagram. According to the strictly mathematical definition, disjoint sets do not exist in Venn diagrams, but we chose to include all the information to show you how the diagram works in general. Commonly, the diagram is used without defining its name, and it is thus not relevant to know the difference for the application only.
Simply said, sets in a Venn diagram always overlap, even if the overlap is empty, because there are no commonalities. In an Euler diagram, however, only realistic overlaps are shown, meaning only those that enclose data.
FAQs
A Venn diagram is a visual representation of data sets and their similarities as well as differences using circles.
Certainly not. In most cases, especially in mathematics, it is common to have only two circles inside a universal set. The Venn diagram is supposed to meet the needs of your topic, so it is your choice how many circles are included.
Yes. In some cases, two sets do not have a common ground and are thus separately depicted.
Of course, theoretically, you can always use ovals in a Venn diagram. However, if you want every set to overlap with each of the others, you need ovals from four sets upwards.