
Accuracy and control are two of the most important things in research methodology, as even the smallest mistake can greatly influence the validity of your study. There are many confounding factors that may affect the dependent variable without being a subject to research, one of them being confounders. The following article will explain this type of variable and everything you need to know about how to avoid them.
Definition: Confounder
Confounders, which can also be called confounding variables or confounding factors, are variables, which influence the independent variable as well as the dependent one. In contrast to a mediator, however, they do not explain the relationship between those, but are an external influence that is not meant to be part of the research. Confounders are often closely related to the independent variable, which makes them easy to overlook in study preparation.
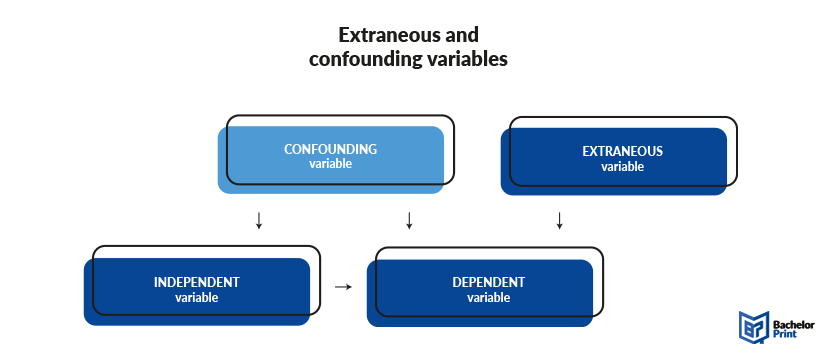
Confounder vs. extraneous variable
The difference between extraneous variables and confounders is very simple. While extraneous variables influence solely the dependent variable, confounders have a relationship with the independent variable as well. Thus, most people define a confounding variable as a type of extraneous variable.
Controling factors
If you want to eliminate confounding variables from your study, there are four main methods to do so. How and where to apply them depends on what you’re studying, the type of sample set used, the complexity of your research, and how many potentially confounding variables are present.
Restriction is a method, where you simply include all possible confounding variables into your study population. Dataset homogeneity lowers the risks of unexpected correlations and causal relationships occurring. This means, that ever influence that could impact your study, is already represented, such as age, gender, income, occupation, family status, etc. depending on which categories might influence your dependent variable.
Matching replicates your initial experiment’s test group and reruns the process to see if the measurable results were meaningful and replicable, or a fluke. Matching can also help create broader and better representative population models via sampling. Matched groups are created by examining the original participants or data points and then identifying new ones that mimic them as closely as possible.
It is also possible to use a control group right from the start, where you then pick a pair, who share the same characteristics and put one in each group. This way, you can compare one group to the other and see, if those dispositions influence your research or not.
Statistical control can be used even after you collected all the data by turning confounding variables into control variables and including them into the results. From your sample, you can establish smaller subgroups with similar values of each confounder, comparing them to each other. However, any confounders you do not know about will not show up this way, and you may still draw wrong conclusions.
Randomization is often considered the best option when it comes to fighting confounders. With this technique, you sample participants randomly into an experimental and control group, making sure that each possible confounder is on an average level in each group. For this method, however, the sample needs to be quite big to ensure that the predispositions and influencing factors are spread equally among the groups.
Usage
Generally, confounding variables are not ideal for your study, since they warp the results and cause them to lose internal validity. On a positive note, confounders always open up possibilities for further research. They may not be what you were looking for this time, but maybe some of your unwanted influences pose rewarding inquiries in the future, leading to valuable new insights.
Other types of variables
- independent variables
- dependent variables
- independent vs. dependent variables
- explanatory vs. response variables
- control variables
- mediator variables
- moderator variables
- mediator vs. moderator
- confounding variables
- extraneous variables
- categorical variables and qualitative variables
- quantitative variables and numerical variables
- nominal variables
- ordinal variables
- discrete variables
- continuous variables
- interval variables and ratio variables
- random variables
- latent variables
- composite variables
- binary variables
FAQs
Confounders are variables that influence the dependent variable as well as the independent one without being a part of the study. They warp the results of a study, oftentimes without the researcher realizing it, creating wrong conclusions in data analysis.
Extraneous variables mostly only influence the dependent variables, or are mainly external influential factors to an experiment. Confounding variables, on the other hand, always influence the independent variables as well and are often closely related to it.
Yes, confounding variables are crucial, as they can influence your study negatively. Confounders are variables, which have an impact on the independent as well as the dependent variable, and are mostly undetected. Thus, they can lead to wrong conclusions in data analysis, as the effect seen on the responder might look like it came from the researched disposition but is in truth induced by a third, undetected source.
Not necessarily. Of course, having a confounder in your study will reduce its validity, which is not desirable. If you find a confounder in your study, there are a few methods explained in this article about how to regain validity.
However, confounding variables can also open up new perspectives for new researches conducted on this topic.
