Cronbach’s alpha is an essential tool for academic research. It is useful for students, publishers and researchers. Cronbach’s alpha may seem like a complicated concept. This post provides an in-depth understanding of Cronbach’s alpha.
In a Nutshell
Cronbach’s α is a method used for measuring the interior constancy of a set or group of items. Below are some of the important things you should know about Cronbach’s α;
- It is an essential concept used in the assessment and evaluation of questionnaires
- It is the most standard degree of inner constancy or reliability
- Cronbach’s alpha is commonly applied when there are several Likert enquiries in a survey or questionnaire
- Cronbach’s alpha is usually reported in scales ranging from 0-1 with the larger values representing more reliability
Cronbach’s alpha: Definition
Cronbach’s alpha is a measure used for assessing the dependability and internal consistency of a set of scales and test items. It can also be described simply as a measure of how closely related a set of items are as a collective. The dependability of given measurements intends the extend to which it is a dependable measure of a concept. Cronbach’s α is an excellent way for measuring the strength of consistency.
Calculate Cronbach’s alpha
The formula for calculating Cronbach’s α is:
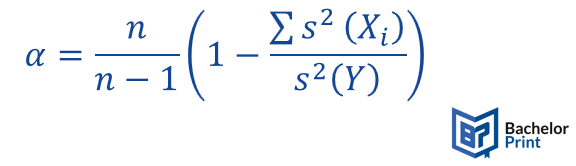
In this case;
- n refers to the number of scale items
- s² (Xi) refers to the variance associated with item
- s² (Y) refers to the variance associated with the observed total scores
Calculate Cronbach’s alpha with SPSS
Below is a step-by-step guide for calculating Cronbach’s α with SPSS:
| Step 1: | Click analyse > scale > reliability analysis (you should find this on the top of the menu). When you do this, you will be presented with a reliability analysis dialogue box |
| Step 2: | The second step is to transfer the variables Qu1 to Qu2 into the items section of the box. You can use the drag and dropping technique to do this |
| Step 3: | Change the Model option set as Alpha. Doing this will instruct SPSS statistics to run the CA |
| Step 4: | Click on the statistics button to receive the reliability analysis in a statistics dialogue box |
| Step 5: | Click on the item, scale, and scale if items deleted sections found in the descriptive area and the correlations options in the inter-item area |
| Step 6: | Click on the continue button to return to the dialogue box for reliability analysis |
| Step 7: | Click OK to generate the output |
Cronbach’s alpha: Interpretation
Once the Cronbach’s α has been calculated, the next natural step is interpreting it. Naturally, a Cronbach’s α of 0.7 of higher is usually considered acceptable. However, when evaluating a scale’s reliability, it is worth considering other factors. Such factors include the face and construct validity of the objects in the measure. Once you have obtained the Cronbach’s alpha value, the next step is to construct an additional analysis. For instance, you may want to conduct an explanatory factor analysis for determining the unidimensionality of the scale. However, there are various assumptions behind this method. These assumptions include;
- Items are ordinal
- The scale is unidimensional
The headmaster suspicion accepts that all things used to compute Cronbach’s α have reactions that follow a request, when contrasted with reactions that follow no request, for example, hair tone or sex. An illustration of an ordinal thing is unified with Likert-scale reaction alternatives, just like the case with the information utilized in this model.
While Cronbach’s alpha can be determined for things that are not ordinal, different tests may be better alternatives to decide a scale’s inward consistency. As to second supposition, a scale is viewed as unidimensional at the point when it estimates just a single fundamental build. On the off chance that a scale gauges more than one basic develop, it is supposed to be multidimensional. This second presumption can be tried utilizing a factor investigation, which decides the number of factors, or measurements, are contained by a bunch of things. On the off chance that a bunch of things isn’t unidimensional, inside consistency may be better estimated by McDonald’s omega.
- ✓ 3D live preview of your individual configuration
- ✓ Free express delivery for every single purchase
- ✓ Top-notch bindings with customised embossing
Negative Cronbach’s alpha
Negative Cronbach’s alpha means that there is inconsistent coding or a mixture of items that measure different dimensions. This results in a negative inter-item correlation. If you get a Negative Cronbach’s α, you can use a factor analysis to check the factorial structure and correlations between the extended factors. You can also have a theory before or prior results to help predict if the results will be positive or negative. Note that Negative Cronbach’s alpha usually violates the reliability model assumption.
Describing Cronbach’s alpha
You can describe Cronbach’s alpha in ranges between 0-1. The highest values normally indicate that the questionnaire or survey is reliable. While describing Cronbach’s alpha, you must include the number of items used on the subscale and the value of Cronbach’s α.
The following is a rule of thumb for describing Cronbach’s α:
| α | Internal consistency |
| >0.9 | excellent |
| >0.8 | good |
| >0.7 | acceptable |
| >0,.6 | questionable |
| >0.5 | poor |
| ≤0.5 | unacceptable |
Dissertation Printing & Binding
You are already done writing your dissertation and need a high quality printing & binding service? Then you are right to choose BachelorPrint! Check out our 24-hour online printing service. For more information click the button below:
Cronbach's alpha - FAQ
Cronbach’s α is a measure of internal consistency. This refers to how closely related a set of items are as a collective. It can also be defined as the measure of scale reliability. Sometimes, Cronbach’s alpha is defined as a purpose of the quantity of items in a test, the average covariance between pairs, and the total score variance.
Tip: If you are done with your academic work, we can help you with thesis printing!
You can use Cronbach’s α to establish that tests and gauges built or implemented for research projects are reliable or to be trusted. You can also use it in science education studies for reporting research scales or ratios and what it represents. It is especially useful in research involving test construction and application.
Yes, you can do this if all of the scale items you wish to analyse are binary. In this case, you will be running an analysis known as the Kuder-Richardson 20 formula. This formula makes it appropriate for objects with scaled replies.
You can calculate Cronbach’s α by correlating each item’s scale with the total score for each individual observation, also known as the individual survey respondents. Later, you can compare the results to the variance for all scores for individual items.
You can report Cronbach’s α in ranges between 0-1. The higher values usually indicate that the survey or report is more reliable. When reporting Cronbach’s alpha , you must include values like the quantity of items applied on a subscale and the value of Cronbach’s alpha.
